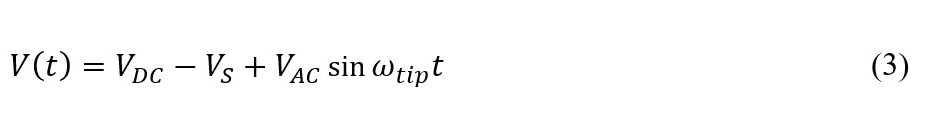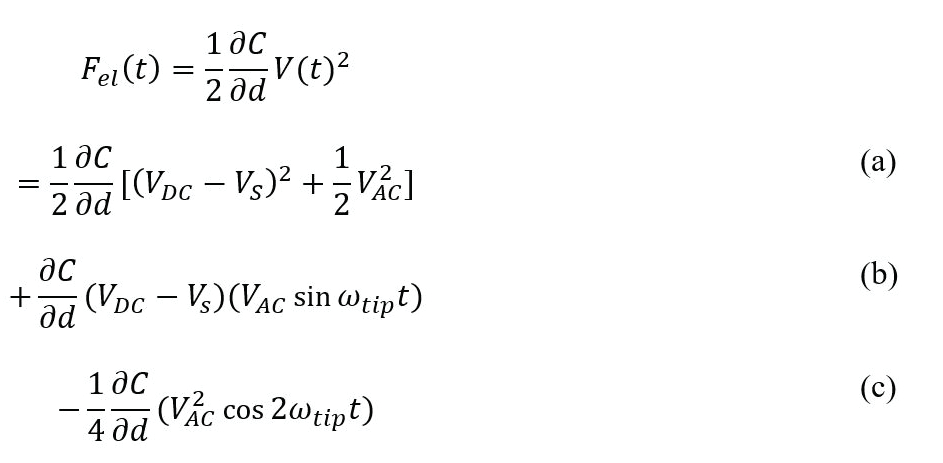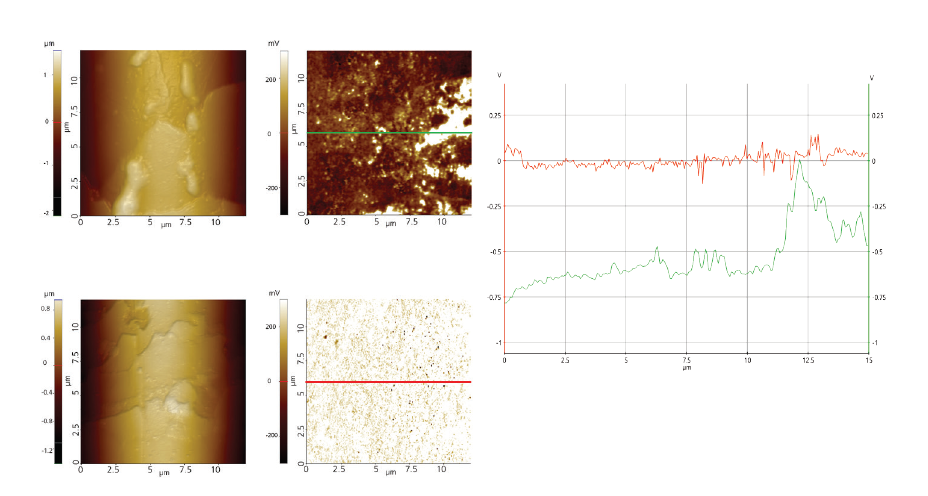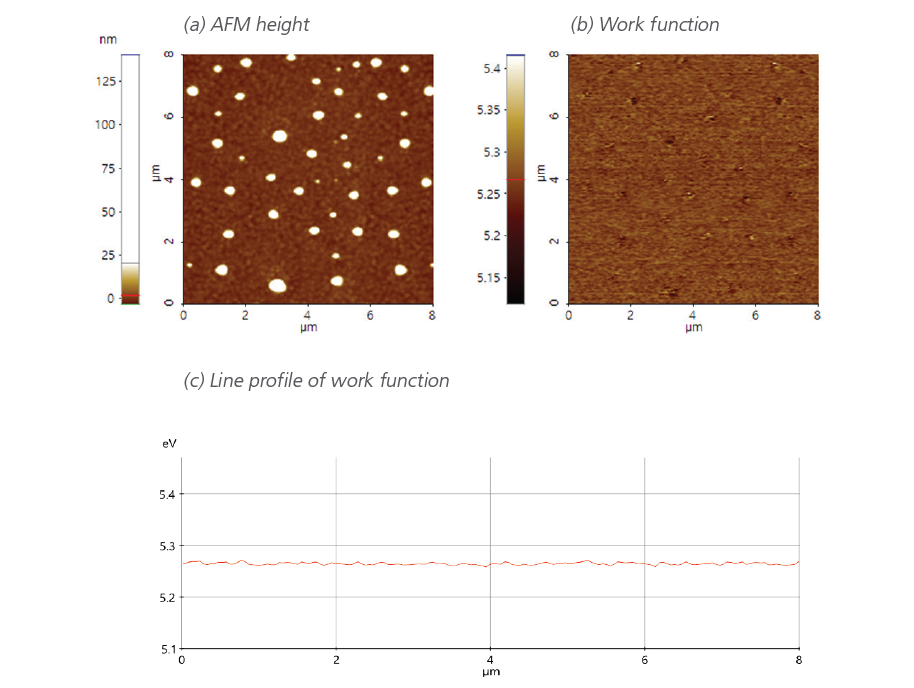
Kelvin Probe Force Microscopy (KPFM)
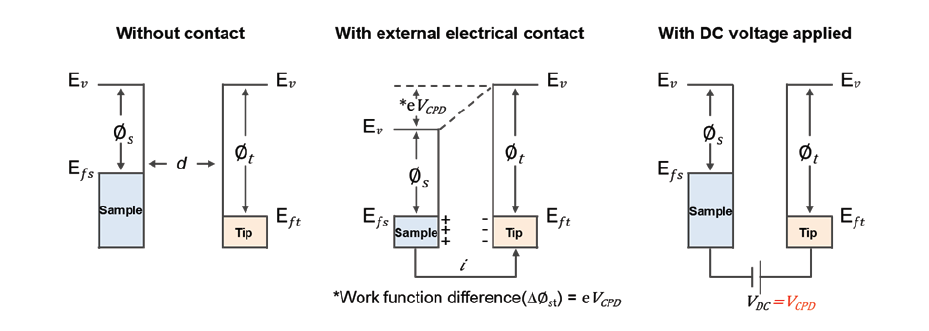
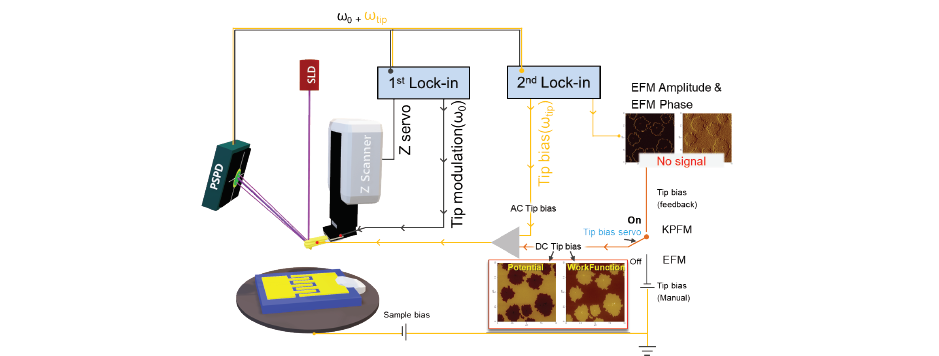
Principle of KPFM is similar to Enhanced EFM with DC bias feedback. DC bias is controlled by feedback loop to zero the ω term. The DC bias that zeros the force is a measure of the surface potential. The difference is in the way the signal obtained from the Lock-in Amplifier is processed. As presented in previous section, the ω signal from Lock-in Amplifier can be expressed as following equation. scanning-kelvin-probe-microscopy-KPFM-f3 The ω signal can be used on its own to measure the surface potential. The amplitude of the ω signal is zero when VDC = Vs, or when the DC offset bias matches the surface potential of the sample. A feedback loop can be added to the system and vary the DC offset bias such that the output of the Lock-in Amplifier that measures the ω signal is zero. This value of the DC offset bias that zeroes the ω signal is then a measure of the surface potential. An image created from this variation in the DC offset bias is given as an image representing the absolute value of the surface potential.